Record for Success

문제 출처: 프로그래머스

문제 설명

🔎 1와 0로 채워진 표(board)가 있습니다. 표 1칸은 1 x 1 의 정사각형으로 이루어져 있습니다. 표에서 1로 이루어진 가장 큰 정사각형을 찾아 넓이를 return 하는 solution 함수를 완성해 주세요. (단, 정사각형이란 축에 평행한 정사각형을 말합니다.)

제한사항
- 표(board)는 2차원 배열로 주어집니다.
- 표(board)의 행(row)의 크기 : 1,000 이하의 자연수
- 표(board)의 열(column)의 크기 : 1,000 이하의 자연수
- 표(board)의 값은 1또는 0으로만 이루어져 있습니다.

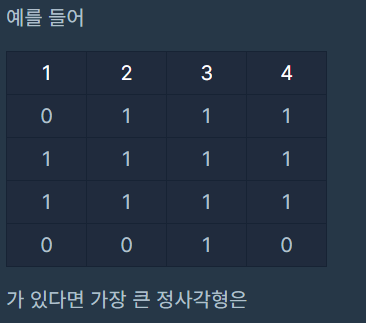
처음에는 이런 방식으로 접근했다.

지금 현재 방문하고 있는 칸이 1이라면, 대각선 아래방향(↘) 을 먼저 확인해 이게 1이라면 대각선 아래의 상,좌를 확인해 사각형이 구성되는지 확인했다.

예제 케이스는 board의 크기가 작기도 하고, 피드백이 바로 가능했기에 맞았지만 테스트케이스는 절반만 맞고 효율성은 통과하지 못했다.

BFS를 통해서 row, column 길이에 제한을 두고 풀어볼까 했지만 이 또한 이전 풀이와 시간복잡도가 다르지 않을 것으로 판단했다.

DP문제라는 힌트를 듣고서 스스로 풀이에 도전했지만, 결국 해답을 찾지 못해 다른 사람들의 도움을 빌려 문제를 해결할 수 있었다.

<정답 코드>

def solution(board):
    answer = 0
    r = len(board) + 1
    c = len(board[0]) + 1
    DP = [[0]*c for _ in range(r)]
    
    for i in range(1, r):
        for j in range(1, c):
            if board[i-1][j-1]:
                DP[i][j] = min(DP[i-1][j], DP[i][j-1], DP[i-1][j-1])+1
            
            answer = max(answer, DP[i][j])
    
    return answer**2

접근은 아래와 같다.

1. board보다 width, hegith가 1씩 더 큰 dp 배열을 만든다.
2. (1, 1)부터 순회를 시작해서 현재 위치가 1에 board에서 1에 해당한다면, 현재 위치의 상, 좌, 대각선 좌측 위(↖) 중에서 가장 작은 값 +1 로 업데이트 한다.

풀이가 생각보다 간단한 것에 놀랬고, 언제 쯤 이런 생각을 바로바로 떠올릴 수 있게 될까 내심 걱정도 됐다.

문제 출처: 프로그래머스

문제 설명

🔎 자연수 x를 y로 변환하려고 합니다. 사용할 수 있는 연산은 다음과 같습니다.

- x에 n을 더합니다.
- x에 2를 곱합니다.
- x에 3을 곱합니다.

자연수 x, y, n이 매개변수로 주어질 때, x를 y로 변환하기 위해 필요한 최소 연산 횟수를 return하도록 solution 함수를 완성해주세요. 이때 x를 y로 만들 수 없다면 -1을 return 해주세요.

아주 전형적인 DP문제였다. 그리고 어디서 풀어본 적도 있는 것 같은 문제였다.

<정답 코드>

def solution(x, y, n):
    answer = 0
    DP = [float('inf')] * (y+1)
    DP[x] = 0
    
    for i in range(x+1, y+1):
        if i < x+n and i < 2*x:
            continue
            
        DP[i] = min(DP[i-n]+1, DP[i])
        
        if i%2==0:
            DP[i] = min(DP[i], DP[i//2]+1)
        
        if i%3==0:
            DP[i] = min(DP[i], DP[i//3]+1)

    return DP[y] if DP[y] != float('inf') else -1

접근은 아래와 같다.

1. 정답을 저장할 DP배열을 만든다. (0부터 시작해도 되고 x부터 시작해도 된다. 편한대로)
2. n의 크기가 지정되어 있지 않으므로 x+n 또는 x*2 중 더 작은 수 부터 순회를 시작한다.
3. i의 크기에 따라 i-n, i//2 (2로 나누어 떨어진다면), i//3 (3으로 나누어 떨어진다면)의 DP 값 중 가장 작은 것 +1로 업데이트한다.

처음에 return 값에서 -1을 처리하지 않고 float 그대로 출력되게 놔두는 실수를 해서 valueError가 발생했었다.

끝까지 집중해서 다 풀자.

문제 출처: 프로그래머스

문제 설명

🔎 N개의 스티커가 원형으로 연결되어 있습니다. 다음 그림은 N = 8인 경우의 예시입니다.

원형으로 연결된 스티커에서 몇 장의 스티커를 뜯어내어 뜯어낸 스티커에 적힌 숫자의 합이 최대가 되도록 하고 싶습니다. 단 스티커 한 장을 뜯어내면 양쪽으로 인접해있는 스티커는 찢어져서 사용할 수 없게 됩니다.

예를 들어 위 그림에서 14가 적힌 스티커를 뜯으면 인접해있는 10, 6이 적힌 스티커는 사용할 수 없습니다. 스티커에 적힌 숫자가 배열 형태로 주어질 때, 스티커를 뜯어내어 얻을 수 있는 숫자의 합의 최댓값을 return 하는 solution 함수를 완성해 주세요. 원형의 스티커 모양을 위해 배열의 첫 번째 원소와 마지막 원소가 서로 연결되어 있다고 간주합니다.

- sticker는 원형으로 연결된 스티커의 각 칸에 적힌 숫자가 순서대로 들어있는 배열로, 길이(N)는 1 이상 100,000 이하입니다.
- sticker의 각 원소는 스티커의 각 칸에 적힌 숫자이며, 각 칸에 적힌 숫자는 1 이상 100 이하의 자연수입니다.
- 원형의 스티커 모양을 위해 sticker 배열의 첫 번째 원소와 마지막 원소가 서로 연결되어있다고 간주합니다.

스티커 모으기1 문제는 풀어보지 않았지만, 이와 비슷한 문제가 백준에서도 존재한다.

문제 유형 자체는 전형적인 DP 문제로 백준의 건물 색칠하기 문제와 유사하다.

문제에서 스티커가 원형이 아니었으면 하나의 DP배열을 이용해서 간단히 해결할 수 있지만, 원형이기 때문에 고려해야 할 사항이 추가된 셈이다.

<정답 코드>

def solution(sticker):
    n = len(sticker)
    if n == 1:
        return sticker[0]
    if n == 2:
        return max(sticker)
    
    dp1, dp2 = [0] * n, [0] * n
    dp1[0] = sticker[0]
    dp1[1] = max(sticker[0], sticker[1])

    dp2[1] = sticker[1]
    dp2[2] = max(sticker[1], sticker[2])

    for i in range(2, n):
        dp1[i] = max(dp1[i - 1], dp1[i - 2] + sticker[i]) if i < n-1 else dp1[i]
        dp2[i] = max(dp2[i - 1], dp2[i - 2] + sticker[i]) if 2 < i else dp2[i]

    return max(max(dp1), max(dp2))

접근 방법은 아래와 같다.

1. 0번 index의 스티커를 사용하는 배열 dp1, 사용하지 않는 배열 dp2를 생성한다.

    1-1. dp1배열은 마지막 스티커를 제외한 n-1개의 스티커를 사용하고, dp2는 0번 스티커를 제외한 n-1개의 스티커를                   사용한다.

2. 각 dp배열에서 처음 사용하게 되는 스티커는 sticker[i]로 초기화 해주고, 두번째로 사용하게 되는 스티커는 첫번째 스티       커와 비교해 더 큰 값으로 지정한다.

3. 앞의 스티커를 사용했을 경우, 바로 다음 스티커는 이용할 수 없으므로 dp[i-1]과 dp[i-2] + sticker[i]를 비교해 max값을      dp[i]에 삽입한다. (1-1을 어기지 않도록 작성한다.)

4. 두 배열 전체에서 가장 큰 값을 리턴한다.

3번의 부연 설명

비슷한 유형의 문제들을 많이 풀고 나니 이와 같은 문제들을 빠른 시간 안에 풀 수 있게 된 것 같다.

문제 출처: 백준 온라인 저지 (https://www.acmicpc.net/problem/1932)

문제 설명

🔎위 그림은 크기가 5인 정수 삼각형의 한 모습이다.

맨 위층 7부터 시작해서 아래에 있는 수 중 하나를 선택하여 아래층으로 내려올 때, 이제까지 선택된 수의 합이 최대가 되는 경로를 구하는 프로그램을 작성하라. 아래층에 있는 수는 현재 층에서 선택된 수의 대각선 왼쪽 또는 대각선 오른쪽에 있는 것 중에서만 선택할 수 있다.

삼각형의 크기는 1 이상 500 이하이다. 삼각형을 이루고 있는 각 수는 모두 정수이며, 범위는 0 이상 9999 이하이다.

처음 문제 예시만 봤을 땐 포화 이진트리나 힙을 생각하게 만드는 문제였다.

하지만 문제를 잘 읽어보면 이진트리 방식으로 수를 선택하면서 내려왔을 때 최대가 되는 수를 출력하는 다이나믹 프로그래밍 문제였다.

<정답코드>

import sys
input = sys.stdin.readline

n = int(input())
tree = []

for i in range(n):
    inp = list(map(int, input().split()))
    if i == 0:
        tree.append(inp)
        continue
    elif i == 1:
        tree.append(list(map(lambda x: x+tree[0][0], inp)))
        continue

    inp[0] += tree[-1][0]
    inp[-1] += tree[-1][-1]

    for j in range(1, len(inp)-1):
        inp[j] += max(tree[-1][j-1], tree[-1][j])

    tree.append(inp)

print(max(tree[-1]))

접근은 아래와 같다.

1. 리스트로 입력을 받아 2차원 리스트 형태로 저장한다.

2. 리스트에 저장하기 전, 각 원소에 대한 부모 노드 중 더 큰 값을 더하여 저장한다.

3. 0번째 리스트는 원래 값 그대로 저장하고, 1번째 리스트는 0번째 리스트의 값만 부모로 갖는다.

트리 구조에 대한 이해만 있다면 쉽게 풀 수 있었던 문제였던 것 같다.

문제 출처 : 프로그래머스 (https://school.programmers.co.kr/learn/courses/30/lessons/42898)

문제 설명

🔎계속되는 폭우로 일부 지역이 물에 잠겼습니다. 물에 잠기지 않은 지역을 통해 학교를 가려고 합니다. 집에서 학교까지 가는 길은 m x n 크기의 격자모양으로 나타낼 수 있습니다.

격자의 크기 m, n과 물이 잠긴 지역의 좌표를 담은 2차원 배열 puddles이 매개변수로 주어집니다. 오른쪽과 아래쪽으로만 움직여 집에서 학교까지 갈 수 있는 최단경로의 개수를 1,000,000,007로 나눈 나머지를 return 하도록 solution 함수를 작성해주세요.

해당 문제는 언듯 보면 BFS 문제인 것 같다는 생각이 바로 들게 만들어 놓은 문제였다. 하지만, 문제를 자세히 읽어보면 최단경로를 도출하는 것이 아니라 최단경로의 개수를 도출하는 문제였다.

나는 거짓말처럼 바로 BFS를 통해 문제 해결을 시도했고.. 처음에는 최단경로 문제인 줄 알고 일반적인 BFS를 구현했지만, 최단경로의 개수라는 것을 인지하고 바꾸어 시도해봤다.

<틀린 코드 보기>

from collections import deque
def solution(m, n, puddles):
    dx, dy = [0, 1], [1, 0]
    maps = [[0] * m for _ in range(n)]
    maps[0][0] = 1
	
    # x, y가 뒤바뀌어서 주어짐;;;
    for x, y in puddles:
        maps[y][x] = -1

    q = deque()
    q.append((0, 0))

    visit = set()
    visit.add((0, 0))

    while True:
        x, y = q.popleft()
        if x == n - 1 and y == m - 1:
            break

        visit.add((x, y))

        for i in range(2):
            nx, ny = x + dx[i], y + dy[i]
            if nx < n and ny < m and maps[nx][ny] != -1:
                q.append((nx, ny))
                maps[nx][ny] = (maps[nx][ny]+1) % (10**9+7)

#    print(*maps, sep='\n')

    return maps[-1][-1]

하지만 결과는 시간초과였다..

문제는 BFS를 통한 방문을 계산하게 되면 같은 좌표에 대한 연산을 방문할 수 있을 때 마다 하는 것이었다.

따라서, 해당 문제의 분류인 다이나믹 프로그래밍으로 접근하여 문제를 해결하였다.

<정답 코드>

from collections import deque
limit = 10**9+7

def solution(m, n, puddles):
    maps = [[0]*m for _ in range(n)]
        
    for x, y in puddles:
        maps[y-1][x-1] = -1
    
    maps[0][0] = 1
    
    for i in range(1, n):
        if maps[i][0] != -1:
            maps[i][0] = maps[i-1][0]
    
    for i in range(1, m):
        if maps[0][i] != -1:
            maps[0][i] = maps[0][i-1]
    
    for i in range(1,n):
        for j in range(1,m):
            a, b = maps[i-1][j], maps[i][j-1]
            if maps[i][j] == -1:
                continue
            
            # 이 부분이 좀 지저분
            if a==-1:
                a=0
            if b==-1:
                b=0
            maps[i][j] = (a+b) % limit
    
    return maps[-1][-1]

접근은 다음과 같다.

문제에선 (우, 하향) 으로 밖에 움직이지 않기 때문에 특정 좌표에 대한 모든 방문 경로가 최단거리임이 보장된다.

1. 1행 또는 1열에 대해서는 방문할 수 있는 경우의 수가 1 밖에 없다. 

2. 1행 또는 1열에 존재하는 웅덩이들은 제외한다.

3. 2행 2열부터 n행m열까지 모든 경로(x, y)에 대해 (x-1, y), (x, y-1)의 값을 더해준다.

이렇게 점화식처럼 이전에 밟을 수 있었던 좌표들 간의 연산을 통해 진행된다는 점이 다이나믹 프로그래밍 스러운 문제였다.

조금 해매기도하고, 출제자의 실수(인지 의도인지 모르겠지만)가 있었기에 풀이하는데 꽤나 오랜 시간이 걸렸다.

하지만, 해당 문제처럼 방문 경로가 반드시 최단거리임이 보장이 될 때 DP로 문제를 해결하는 방법에 대해 배울 수 있어서 좋았다.