[프로그래머스] 합승 택시 요금 (파이썬)

문제 출처: 프로그래머스

프로그래머스

 

문제 설명

🔎 [본 문제는 정확성과 효율성 테스트 각각 점수가 있는 문제입니다.]
밤늦게 귀가할 때 안전을 위해 항상 택시를 이용하던 무지는 최근 야근이 잦아져 택시를 더 많이 이용하게 되어 택시비를 아낄 수 있는 방법을 고민하고 있습니다. "무지"는 자신이 택시를 이용할 때 동료인 어피치 역시 자신과 비슷한 방향으로 가는 택시를 종종 이용하는 것을 알게 되었습니다. "무지"는 "어피치"와 귀가 방향이 비슷하여 택시 합승을 적절히 이용하면 택시요금을 얼마나 아낄 수 있을 지 계산해 보고 "어피치"에게 합승을 제안해 보려고 합니다.

출처: 프로그래머스

출처: 프로그래머스

---

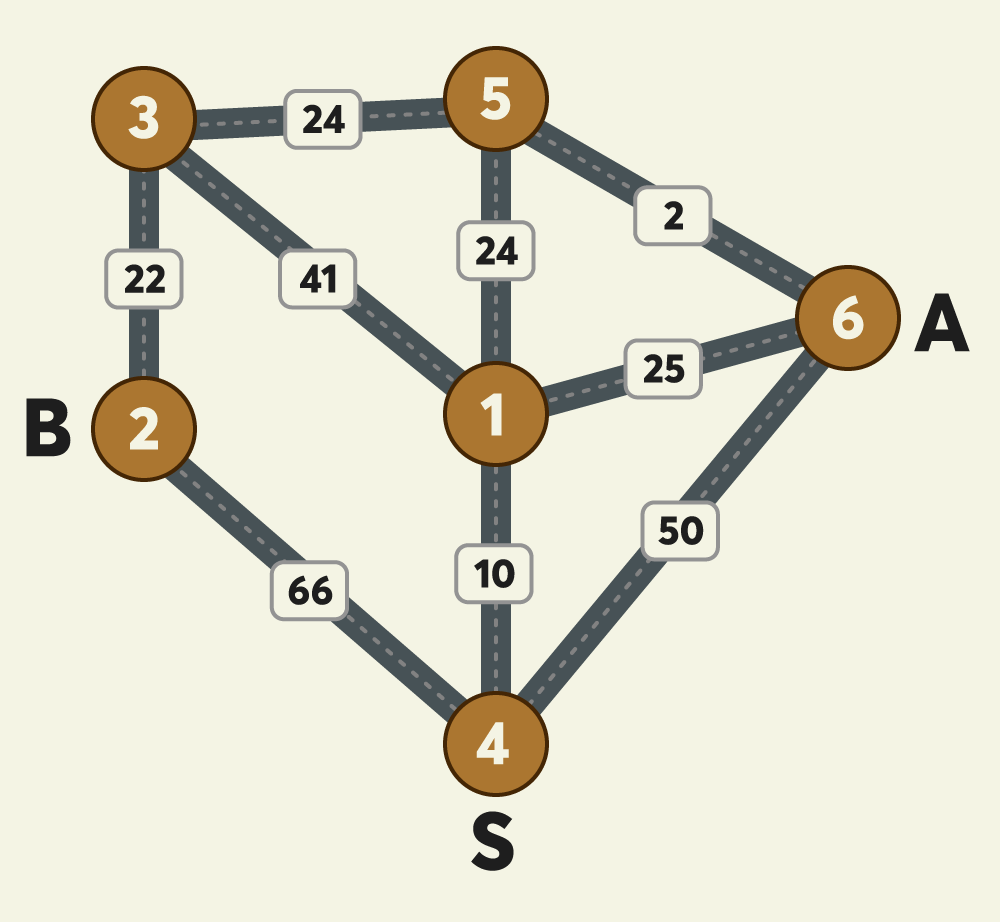
최단거리, 최저비용이라는 맥락에서 한가지 알고리즘을 떠올리는 것 자체는 어렵지 않으나 거기서 한단계 더 나아가야한다는 부분이 어려웠던 문제였다.

 

문제를 읽고 '다익스트라' 를 사용해야겠다 마음을 먹고,

s로 부터 a와 b까지의 최단 경로를 구해서 겹치는 부분의 비용을 제거하면 된다고 생각했으나, 그것과는 별개인 문제였다.

당장에 주어진 예시만 봐도 S -> A는 4->1->6이 최단경로고, S->B는 4->2가 최단거리였다. 여기서 겹치는 구간은 없었으나, 5까지 함께하면 더 저렴한 비용으로 갈 수 있었다.

 

한참을 고민하다가 결국 검색을 했었고, 생각보다 간단한 원리에 감탄했고 한번 더 배울 수 있었다.

 

<정답 코드>

from queue import PriorityQueue
def solution(n, s, a, b, fares):
    answer = float('inf')
    road = [[] for _ in range(n+1)]
    
    for u, v, cost in fares:
        road[u].append((v, cost))
        road[v].append((u, cost))
    
    def dijkstra(x):
        dist = [float('inf')] * (n+1)
        dist[x] = 0
        q = PriorityQueue()
        q.put((0, x)) # cost, 도착지, 출발지
        
        while q.qsize() > 0:
            cur = q.get()
            _x = cur[1]
            
            for nx, cost in road[_x]:
                if dist[_x] + cost < dist[nx]:
                    dist[nx] = min(dist[nx], dist[_x] + cost)
                    q.put((dist[nx], nx))
        
        return dist
    
    #----------------참고 코드----------------#
    dist = [[]]
    
    for i in range(1, n+1):
        dist.append(dijkstra(i))
        
    for i in range(1, n+1):
        answer = min(answer, dist[s][i] + dist[i][a] + dist[i][b])
    
    return answer

접근은 아래와 같다.

1. 모든 노드에 대해 각 지점 별 최단비용 거리를 다익스트라 함수로 구한다.
   1. 이를 기록하는 dist 배열은 빈 배열이 하나 추가된 상태로 구현한다. (index=0에 해당하는 노드가 존재하지 않기 때문)
2. 모든 노드의 최단거리 목록을 순회하면서,  S-> i, i->A, i->B를 모두 더한 값 중 최소가 되는 값이 정답이다. (i = 현재 순회중인 노드)

 

모든 경로에 대한 다익스트라 배열을 구한다는 것을 생각해내지 못해 스스로는 풀지 못했던 문제다.

 

레벨별 문제에 슬슬 익숙해지려 하니, level3문제들이 대체로 기본 알고리즘 + 한 단계 발전인 느낌이 드는 것 같다. 재미있다.

 

대체로 빠른 속도를 내는 O(E logV)의 시간복잡도를 가진 다익스트라 함수였지만, 꽤 오래걸리는 예제도 있었다.

 

오히려 O(n³)의 시간복잡도를 가진 플로이드-와샬 알고리즘이 더 빨리 작동할 수 있다는 글을 보아 아래에 정리했다.

---

플로이드-와샬 알고리즘 풀이

 

플로이드 와샬 : i에서 k를 거쳐 j로 가는 최단거리를 구하는 알고리즘, 3중 반복문을 사용하기 때문에 O(n³)의 시간복잡도를 갖는다.

 

<플로이드 와샬 풀이>

def solution(n, s, a, b, fares):
    answer = float('inf')
    cost = [[float('inf')] * (n+1) for _ in range(n+1)]

    # cost 중에서 fares에서 제시된 도로
    for u, v, _cost in fares:
        cost[u][v] = _cost
        cost[v][u] = _cost

    #플로이드 와샬 알고리즘
    for k in range(1, n+1):
        for i in range(1, n+1):
            for j in range(1, n+1):
                if i == j:
                    cost[i][j] = 0
                else:
                    cost[i][j] = min(cost[i][j], cost[i][k] + cost[k][j])


    for i in range(1, n+1):
        answer = min(cost[s][i] + cost[i][a] + cost[i][b], answer)

    return answer

다익스트라에서 dist로 구현되었던 전체 구간에 대한 비용을 cost로 작성하였다.

 

1. fares에서 제시된 노드 간의 연결은 해당 비용으로 업데이트 해준다.
2. cost 배열에서 서로 다른 상수 i, j에서 i -> j의 비용 중에서 i -> k -> j로 방문했을 때 더 저렴한 경우 그 비용으로 업데이트 해준다. (반복문의 순서를 바꾸면 다르게 작동하므로 순서에 유의)

이후의 과정은 다익스트라와 동일하다.

 

평균적인 속도는 다익스트라보다 느리게 작동하지만, 최대의 경우에도 2600ms 이내에 해결한다는 것에서 의미가 있는 풀이었다.