[프로그래머스] 쿼드압축 후 개수 세기 (파이썬, 분할정복)

문제 출처: 프로그래머스

프로그래머스

 

문제 설명

🔎0과 1로 이루어진 2n x 2n 크기의 2차원 정수 배열 arr이 있습니다. 당신은 이 arr을 쿼드 트리와 같은 방식으로 압축하고자 합니다.

구체적인 방식은 다음과 같습니다.

당신이 압축하고자 하는 특정 영역을 S라고 정의합니다.
만약 S 내부에 있는 모든 수가 같은 값이라면, S를 해당 수 하나로 압축시킵니다.
그렇지 않다면, S를 정확히 4개의 균일한 정사각형 영역(입출력 예를 참고해주시기 바랍니다.)으로 쪼갠 뒤, 각 정사각형 영역에 대해 같은 방식의 압축을 시도합니다.

arr이 매개변수로 주어집니다.
위와 같은 방식으로 arr을 압축했을 때, 배열에 최종적으로 남는 0의 개수와 1의 개수를 배열에 담아서 return 하도록 solution 함수를 완성해주세요.

출처: 프로그래머스

 

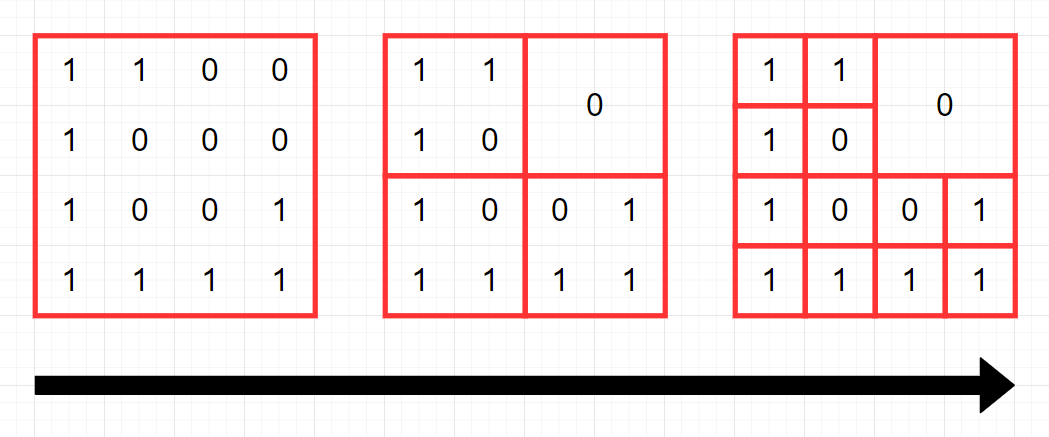
정사각형의 크기를 가진 2차원 배열을 4분할 하면서 풀어나가는 문제다.

 

처음에는 배열을 분할하는데 초점을 두고 문제를 풀어보려했다.

배열의 크기는 반드시 2의 배수인 정사각형 형태였기 때문에 항상 (배열의 길이)//2 만큼씩 행, 열을 분할해서 진행해나가면 4분할 하는 것은 그렇게 어렵지 않았다.

 

하지만, 분할된 사각형 안에서 0과 1의 개수를 세아리는 부분이 어렵다.

처음에는 재귀호출을 통해 분할이 불가능할 때 까지 분할한 후 list로 반환하는 답안을 작성하였다.

 

<틀린 코드 보기>

def quard_split(arr):
    n = len(arr)
    box = [[], [], [], []]
    for i in range(n//2):
        box[0].append(arr[i][:n//2])
        box[1].append(arr[i][n//2:])
        box[2].append(arr[n//2+i][:n//2])
        box[3].append(arr[n//2+i][n//2:])
        
    for i in range(4):
        if 0 < sum(list(map(lambda x: sum(x), box[i]))) < (n//2)**2:
            box[i] = quard_split(box[i])
    
    return box

def solution(arr):
    answer = [0, 0]
    box = quard_split(arr)
    print(box)
    return answer

 

분할을 한 결과 배열을 출력해보면 위와 같이 중첩 배열 형식으로 나타나기 때문에 이것을 다시 flatten 하는 작업이 어려웠고, flatten했을 때 하나로 세아려지는 0, 1의 개수를 파악하기가 어려웠다. 그렇다고 무작정 for문을 돌리자니 깊이가 얼마인지 알 턱이 없었기 때문에 시간 복잡도 부분에서도 심각한 문제가 있었다.

 

정답에서는 실제로 분할하는 것이 아닌, count하는 것이 주 목적이었다.

 

<정답 코드>

def solution(arr):
    answer = [0, 0]
    _len = len(arr)
    
    def quard_split(x, y, _len):
        cur = arr[x][y]
        
        for i in range(x, x+_len):
            for j in range(y, y+_len):
                if arr[i][j] != cur:
                    _len //= 2
                    quard_split(x, y, _len)
                    quard_split(x+_len, y, _len)
                    quard_split(x, y+_len, _len)
                    quard_split(x+_len, y+_len, _len)
                    return
        
        answer[cur] += 1
    
    quard_split(0, 0, _len)
    return answer

이 방법은 분할을 모두 마친 후 분석을 진행하는 것이 아닌, 분할을 하는 과정에서 count를 한다. 다른 개념 자체는 이전에 작성했던 코드와 일치한다.

 

접근은 아래와 같다.

1. 분할(혹은 전체) 사각형의 좌측 상단 꼭짓점을 좌표에서 시작해서 해당 사각형 내에서 시작점과 다른 값을 하나라도 가지면 다시 4분할을 진행한다.
2. 반복문을 전부 순회하고 탈출하게 되면 시작점 값을 +1 해준다.

🔎해당 알고리즘은 분할 정복 알고리즘이라고 한다.
쉽게 풀리는 부분은 그냥 계산으로 진행하고, 아니면 작은 여러 개의 부분 문제로 구분해서 푸는 개념이다.
위 문제에서는 하나의 사각형을 점검하는 quard_split 함수가 분할해야 하는 상황에 처하게 되면 4개의 quard_split함수로 나뉘어 문제를 푸는 형태인 것이다.

 

코딩 테스트를 공부하다 보면 가장 자주 등장하는 탐색, DP, 트리, 그래프 등의 문제 이외에도 분할 정복, 이분 탐색, 슬라이딩 윈도우 등과 같이 한번씩 등장하는 어려운 문제들을 발견할 수 있다.

 

이런 문제일수록 더욱 꼼꼼히 기록하고 기억해서 코딩 테스트에서 우위를 가져갈 수 있도록 노력해야겠다.